The persistent currents for the parafermion Hall states, the Fermi liquid
and the Laughlin state with nu=1/3
In this page I present several figures of the persistent currents computed
within the CFT for the parafermion (PF_k) fractional quantum Hall (FQH)
states in the second Landau level and compare them to the currents in the
Fermi liquid and the Laughlin FQH state.
The general conformal field theory (CFT) approach to the persistent
currents has been described in hep-th/0408052. The details for the
analysis of the persistent currents in the parafermion FQH states can be
found in Phys. Rev. B 69, 085305 (2004).
I have used Maple to differentiate analytically the CFT partition functions
and then have computed numerically the amplitudes of the currents for different
temperatures.
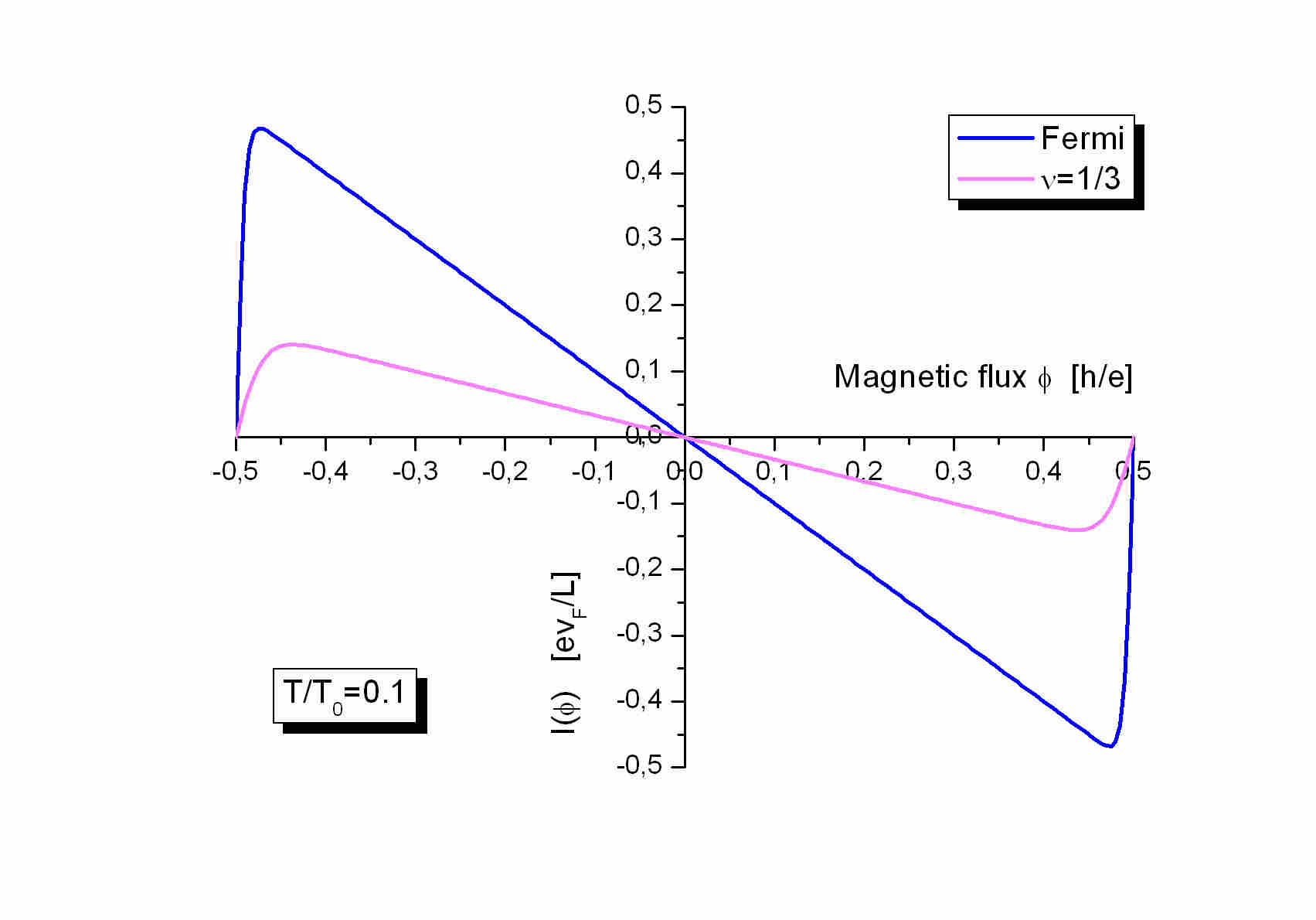
The periods:
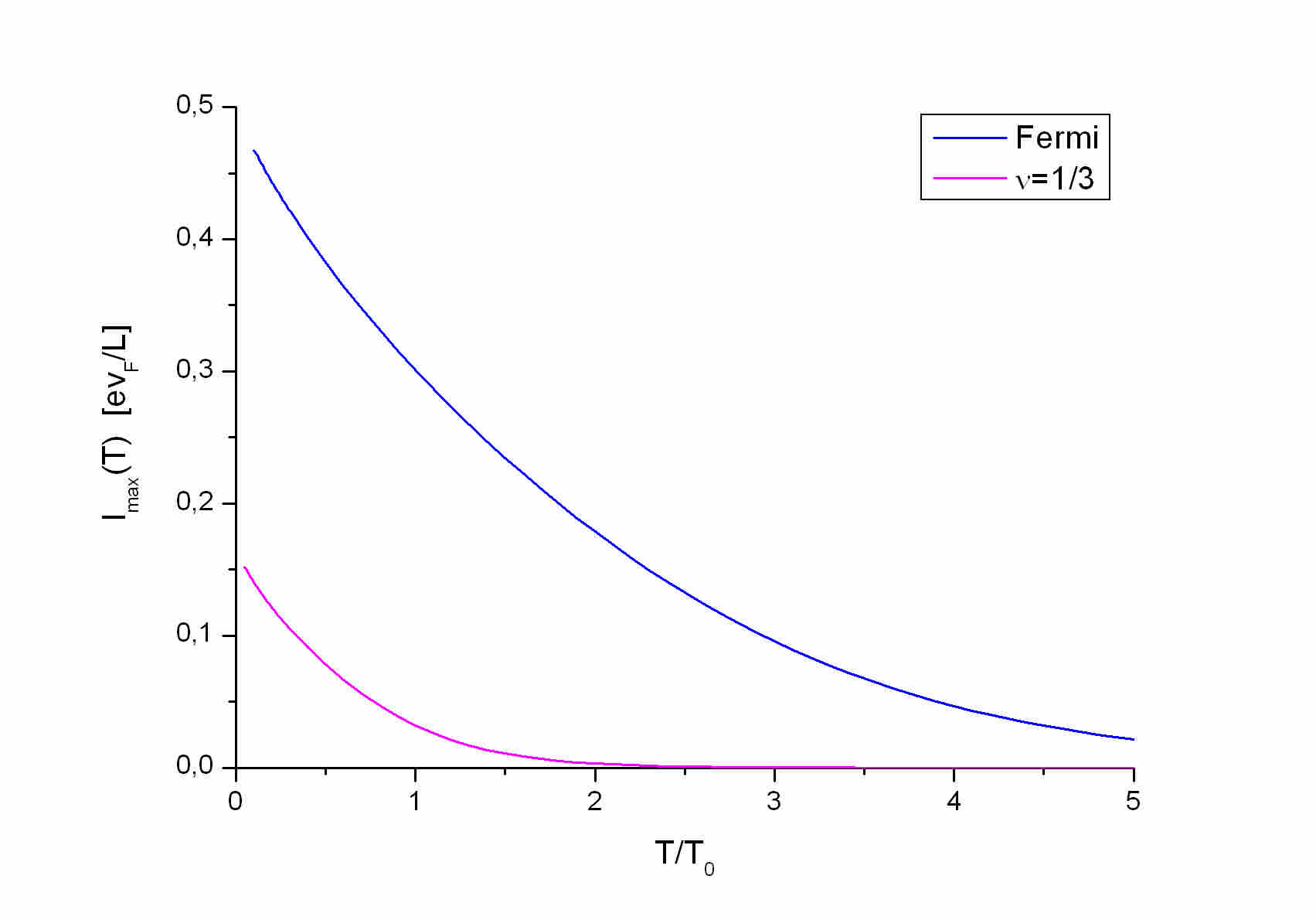
The persistent currents in the Fermi liquid and Laughlin states
are periodic functions of the magnetic flux with period 1. This is in agreement
with the Bloch-Byers-Yang theorem.
The currents are measured in units ev_F/L where e is the electron charge,
v_F is the Fermi velocity on the edge and L is the circumference of the
edge and their amplitudes are proportional to the filling factors. The
temperature is measured in units of T_0=h v_F/2 pi^2 k_B L, where
k_B is the Boltzmann constant and the next two figures correspond to T/T_0=0.1..
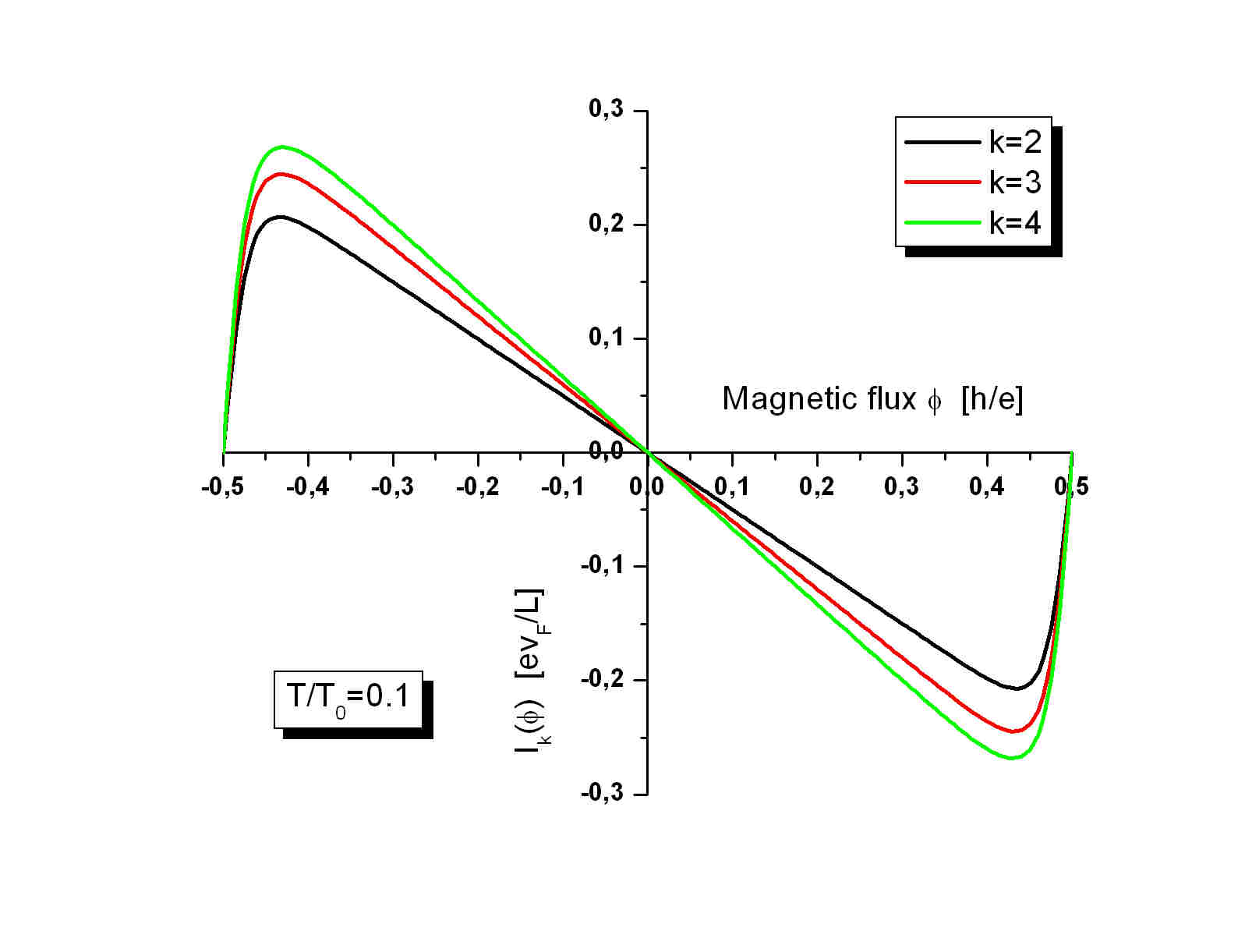
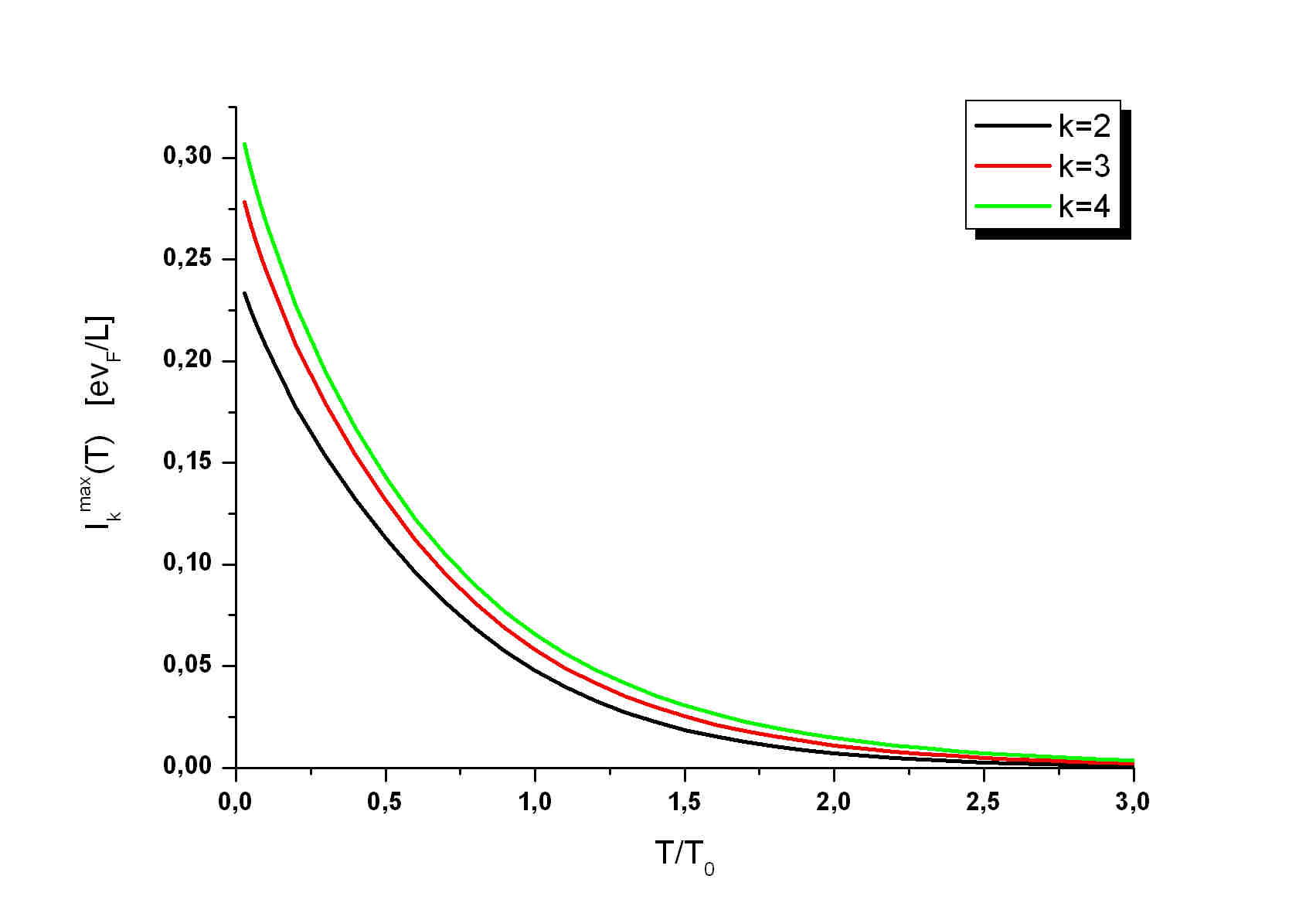
The PF_k states:
The periods of the persistent currents in the parafermion FQH states
is again 1 flux quantum h/e.
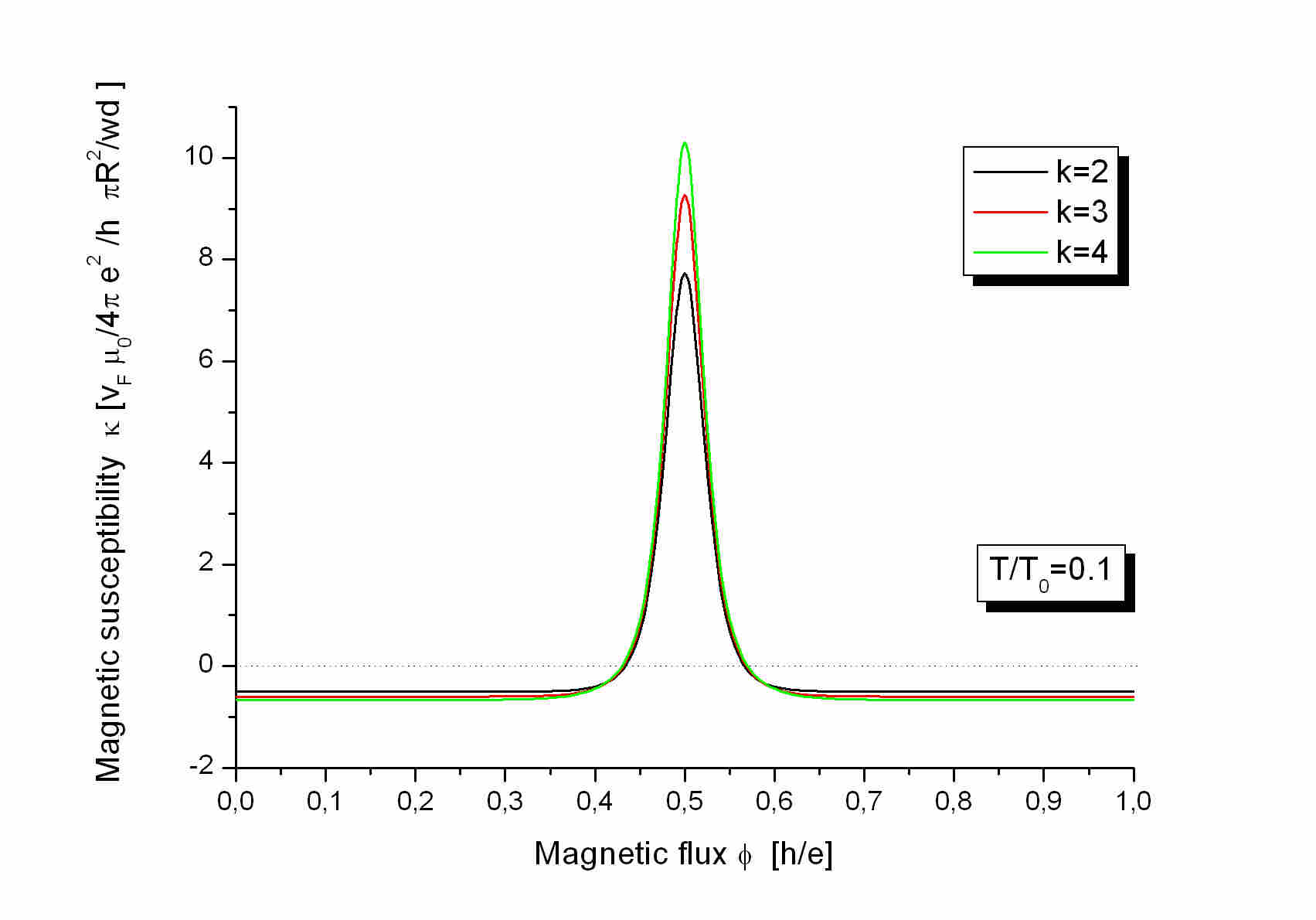
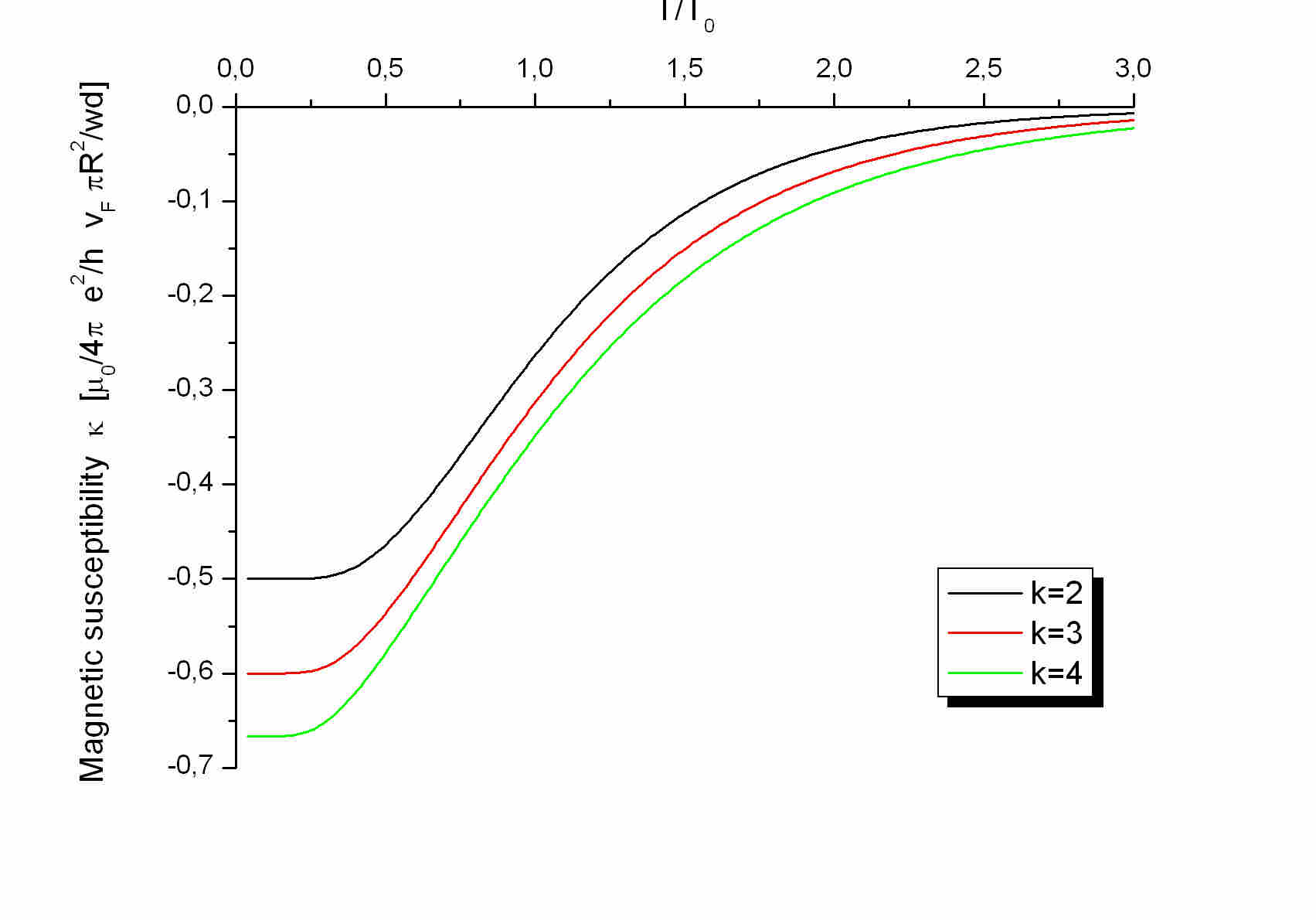
The magnetic susceptibility in the PF_k states:
Because the persistent currents are proportional to the Aharonov-Bohm magnetization
I have computed the magnetic susceptibility as a derivative of the current,
see Phys. Rev. B 69, 085305 (2004). The susceptibility is also periodic
with period one flux quantum and I plotted it in the interval [0,1].
The amplitude decay:
The persistent currents are thermally suppressed due to different mechanisms
at different temperatures. At low temperature, T<<T_0, the
amplitudes decay logarithmically due to the thermal activation of quasiparticle-quasihole
pairs. At high temperatures, T>>T_0, however, the main mechanisms are the
thermal smearing and decoherence which lead to an exponential decay of
the persistent currents amplitudes.
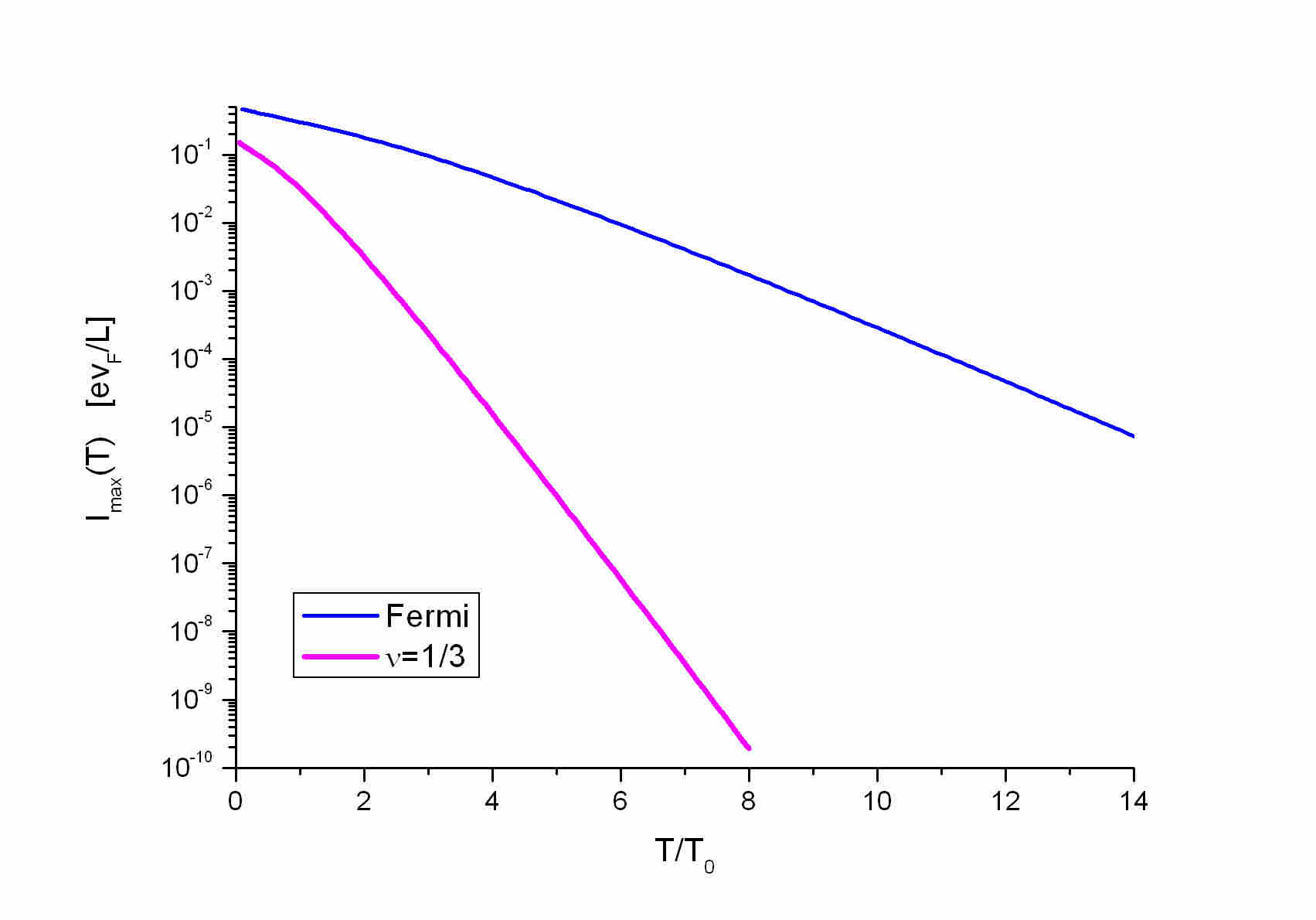
The Fermi-Lauglin states:
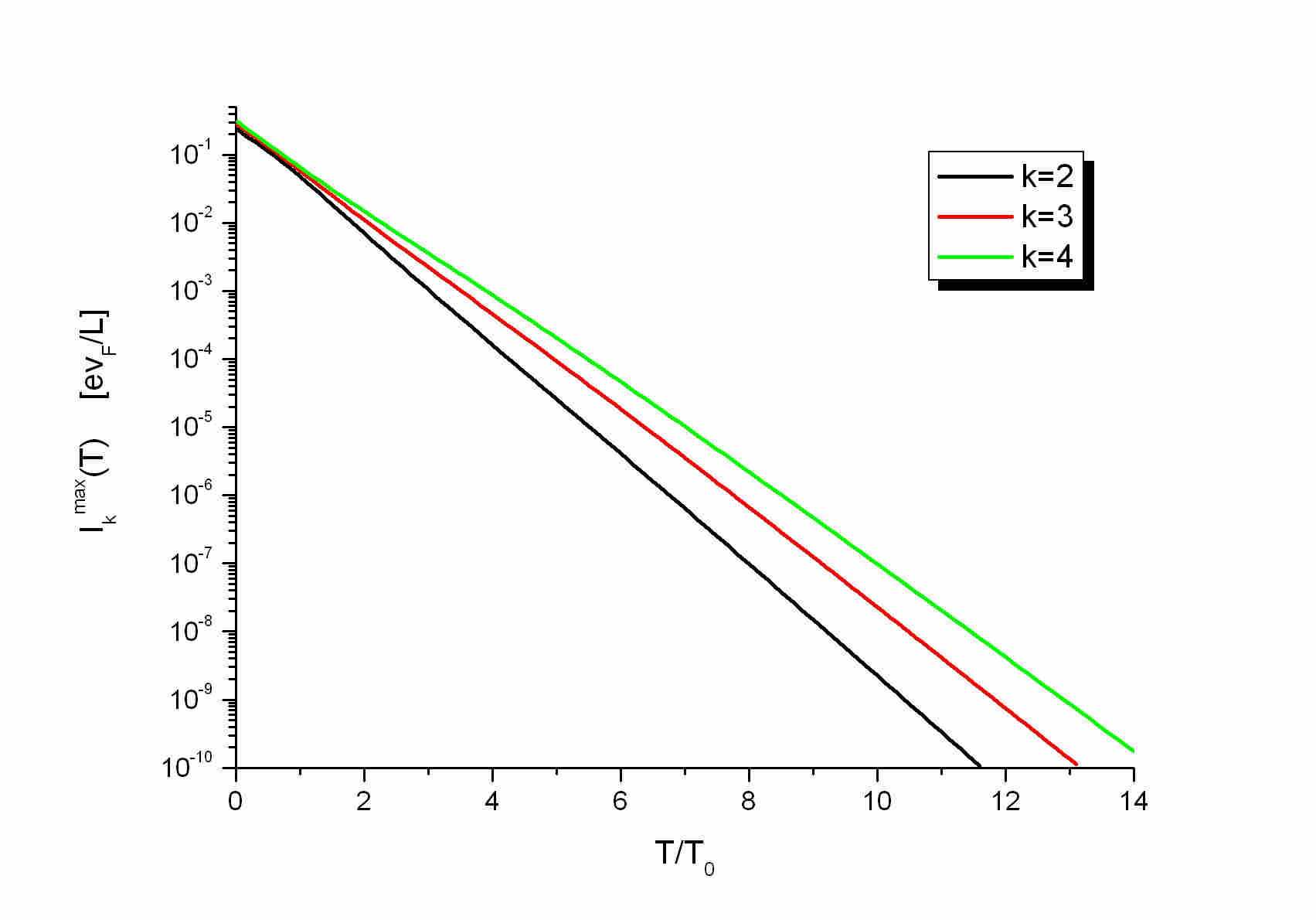
The PF_k states:
The susceptibility decay in PF_k states:
The susceptibility also decays with increasing the temperature and it shows
very well the two different decay regimes.
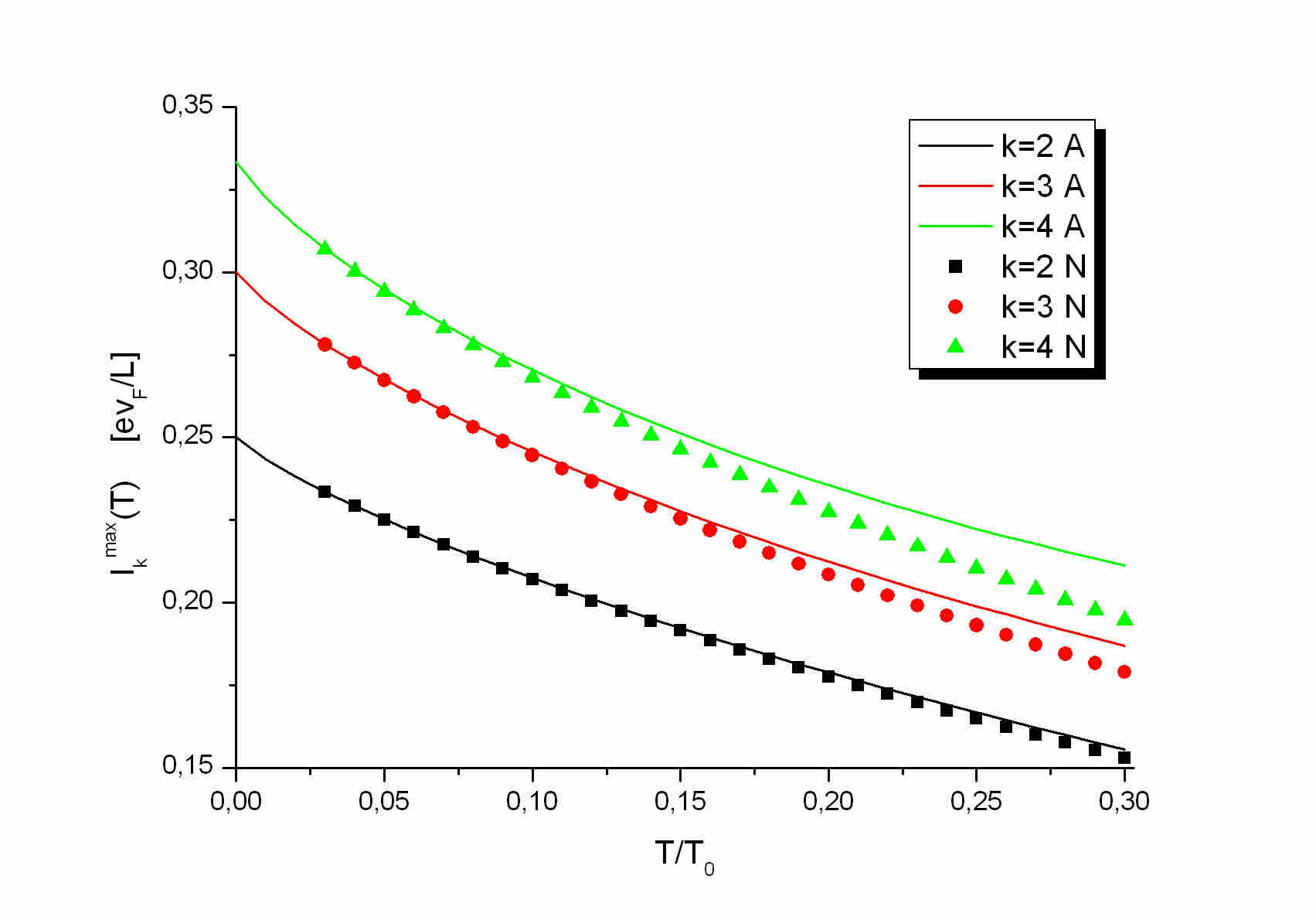
Low-temperature asymptotics in the PF_k states:
In the next figure I compare the exact numerical calculations (black boxes,
red circles and green triangles) of the persistent currents amplitudes
in the PF_k states with the asymptotic analytic formulas (black, red and
green solid lines) for low temperatures derived in Phys. Rev. B 69, 085305
(2004). Obviously the asymptotic analytic formulas are in very good agreement
with the exact numerical data for T/T_0 <0.1.
Logarithmic plots:
Due to the exponential decays of the persistent currents it is more convenient
to plot the current's amplitudes ina (semi) logarithmic plot. The high-temperature
asymptotics formulas of the currents can be seen in hep-the/0408052 and
in Phys. Rev. B 69, 085305 (2004). They contain a ln(T/T_0) contribution
plus a stright line with negative slope from the the exponentials. This
slope is the fingerprint of the FQH state.
Fermi-Laughlin states:
The PF_k states:
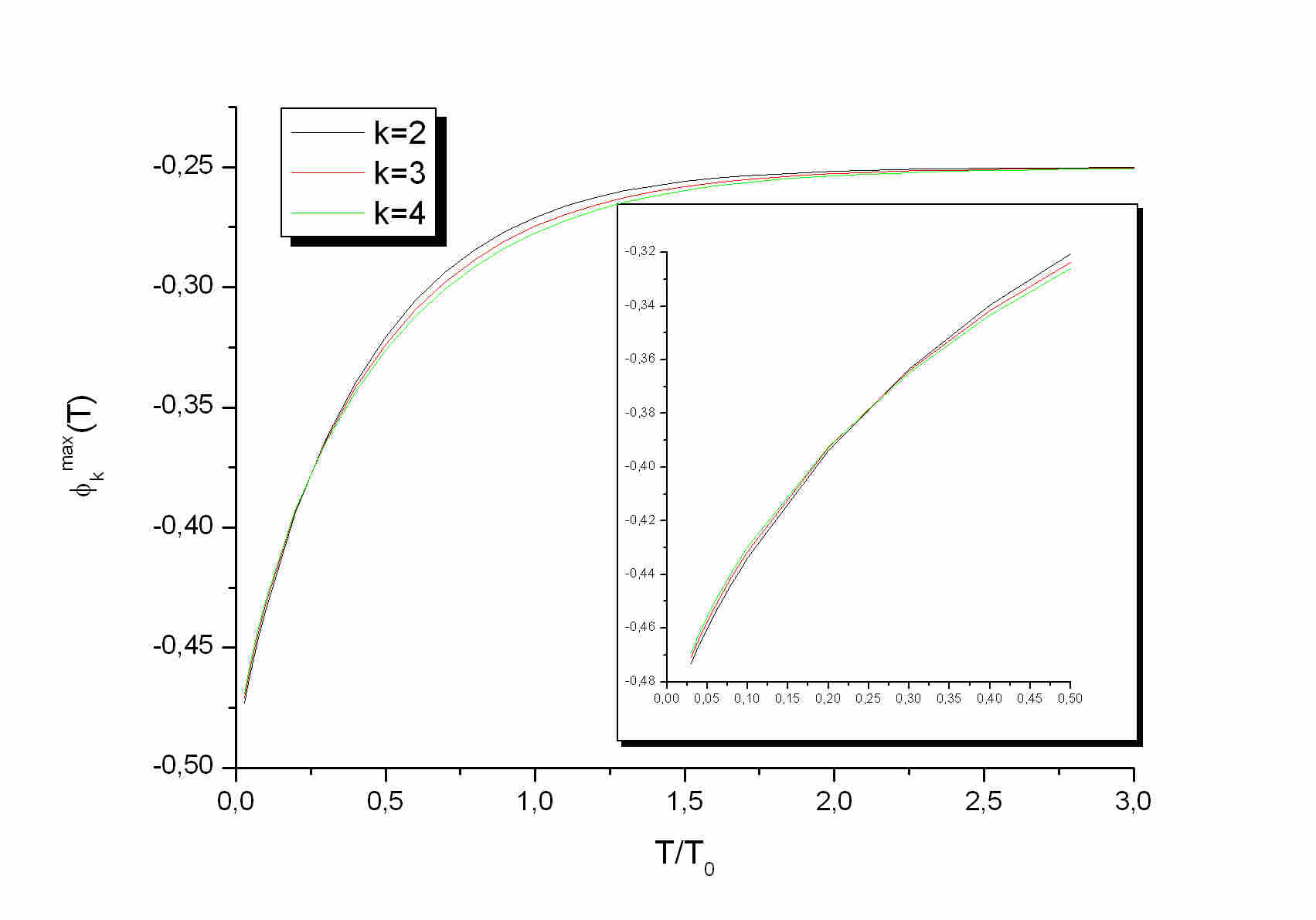
Phi_max in the PF states:
In the next figure we show how the position of the maximum of the persistent
current changes with temperature for
0.03<T/T_0<3. For very low temperatures phi_max -> 1/2 while
for higher temperatures phi_max -> 1/4.