Animations

In this page you can find animations of the electron charge and current densities for a two-dimensional electron gas in a quantum Hall ring
of major radius R and width 2a. For a more detailed explanation see  cond-mat/0404681.

The electron charge density , measured in units of , is plotted in red color in Animation 1 as a function of the radial coordinate  between -150 and 150 (in units of )  measured from the major radius  of the quantum Hall ring, where  is the avearge interparticle spacing. The constant positive background charge density has a trapezoid shape as plotted with blue color in the same units on Animations 1, 2 and 3. All animations have been produced from data computed numerically by Hartree method at temperature
= 0.005 in units of  where  is the dielectric constant.

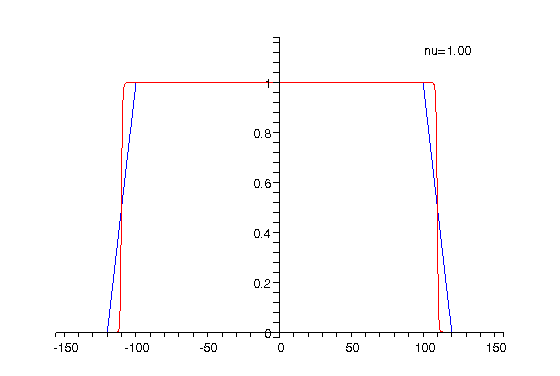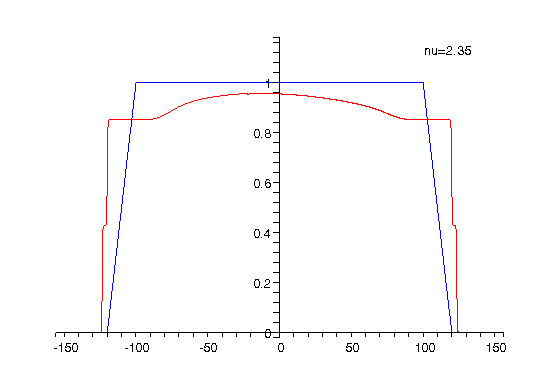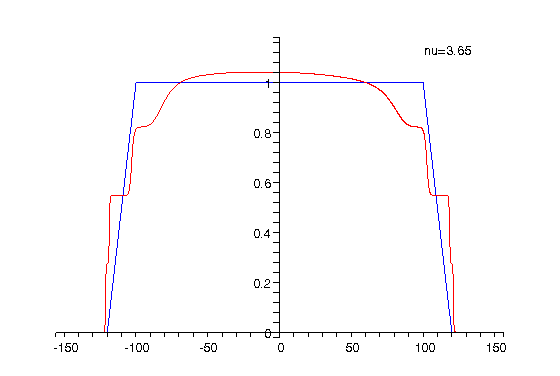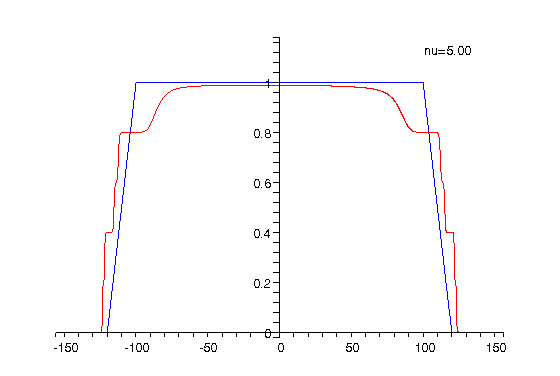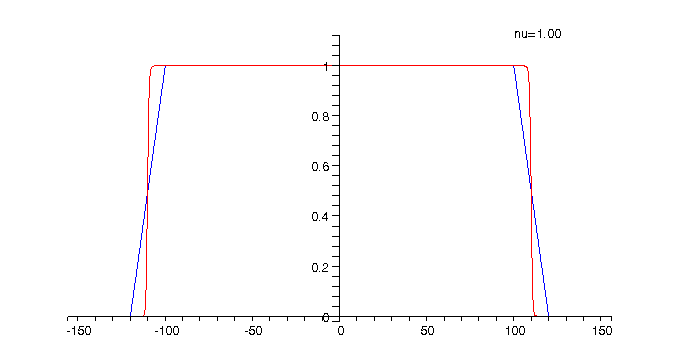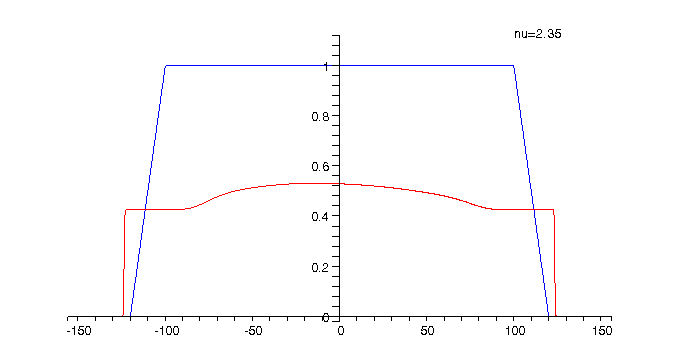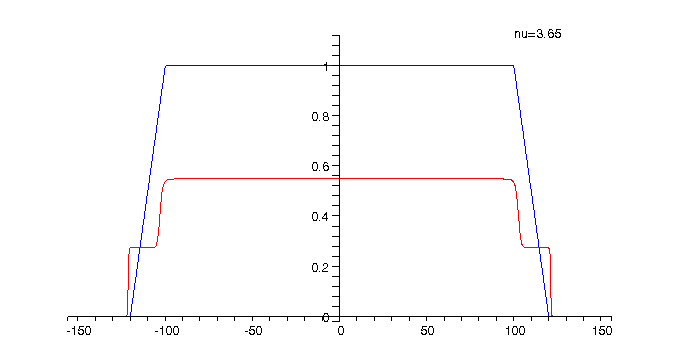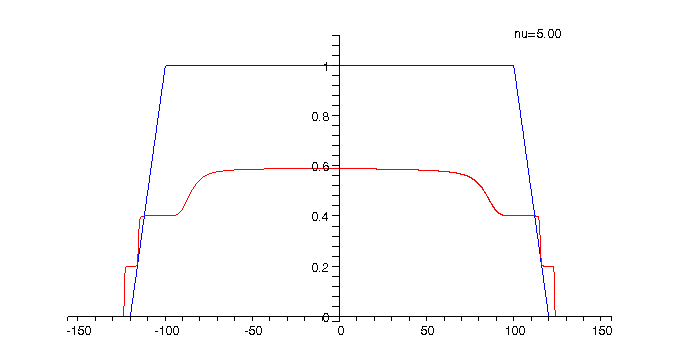
Animation 1: The electron charge density for  The animation shows how the charge density changes when the filling factor increases from 1 to 5 and displays wide incompressible channels (corresponding to the step-like formations in the density)  at the inner and outer edges of the ring sample when the filling factor  takes integer values. Note that the charge density is slightly asymmetric, i.e., n(-x) is different from n(x), which is more obvious when is fractional. This is because the electron system is not precisely in the de Haas-van Alphen limit R >> a.

Because the Zeeman gap is only about 25% of the cyclotron energy the incompressible strips formed at odd integer  are narrower than those at even integer filling factors which is evident in Animation 1.
 
 

The charge density shown in Animation 1 is computed as the sum of the partial densities corresponding to spin up and down. Because the magnetic field B (whose magnitude is inversly proportional to ) is parallel to the z axis the majority of the electrons would have spin up.  The evolution of the spin-up density with the filling factor is shown in Animation 2, while that of the spin-down electrons is displayed on Animation 3.
 

	Animation 2: The charge density for spin-up electrons The spin-up density is shown in red and is compared to the trapezoid-shaped positive background charge density which is plotted in blue.

 
 
 

Animation 3: The charge density for spin-down electrons   The spin-down density is shown in red and is compared again to the trapezoid-shaped positive background charge density which is plotted in blue.

 
 

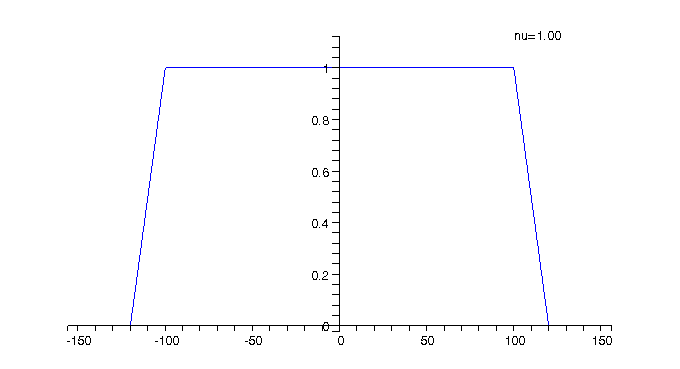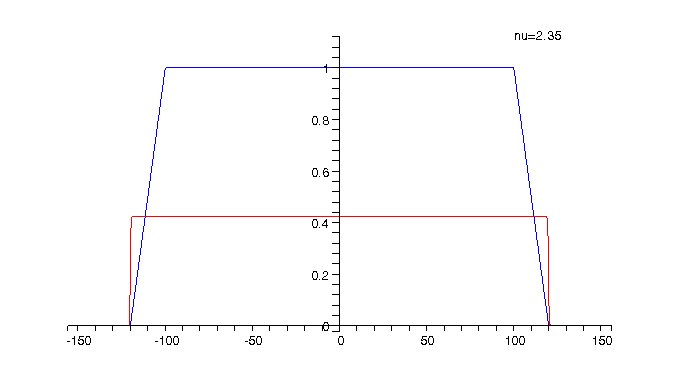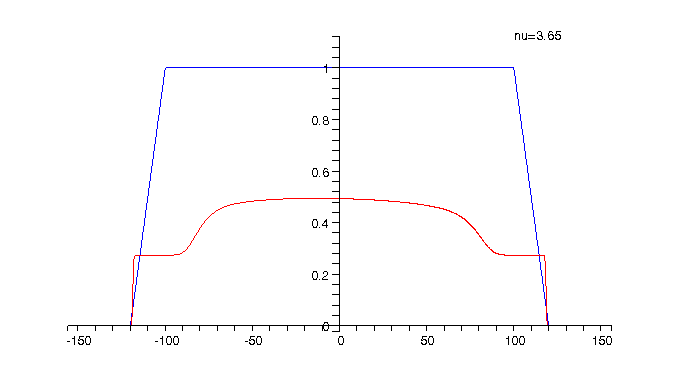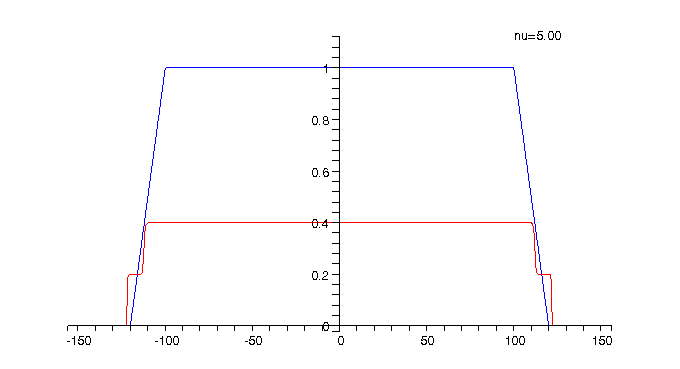
Animation 4:  The current density for 
The current density , measured in units of  , which has both edge and bulk components that are computed as certain radial derivatives of the charge density and Hartree potential, is plotted bellow as a function of the radial coordinate  .The red curve shows how the current density evolves as the filling factor is changed from 1 to 5 . The blue colored curve shows for comparison the current density at and can be used to mark the two edges of the two-dimensional quantum Hall ring.

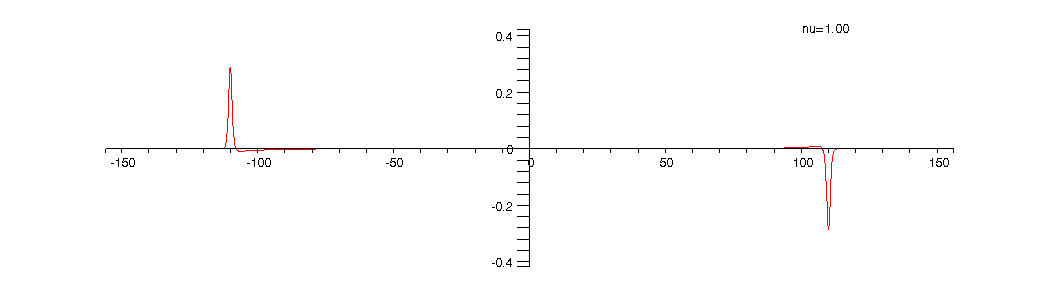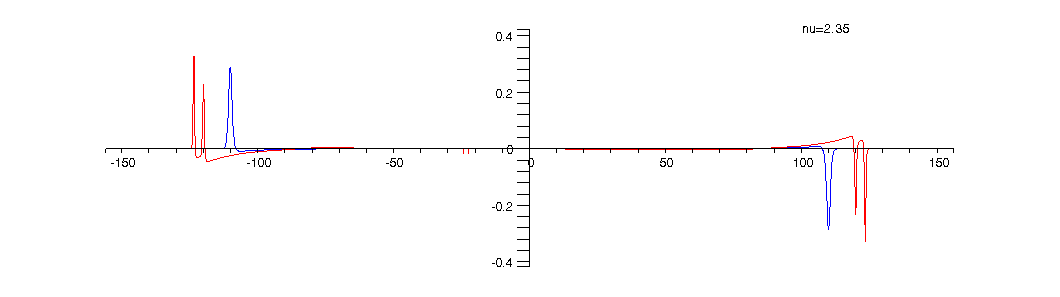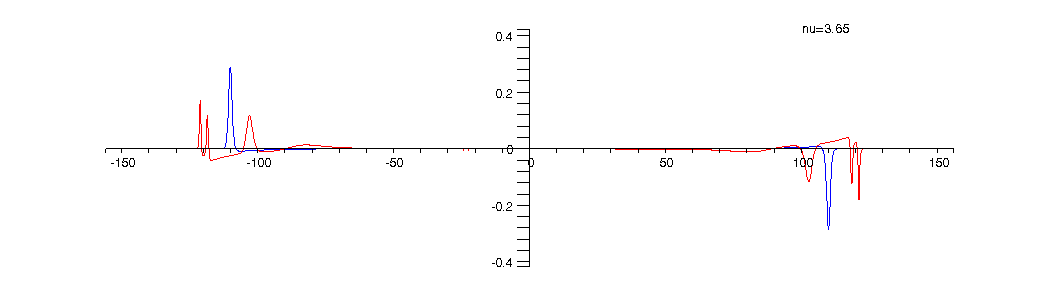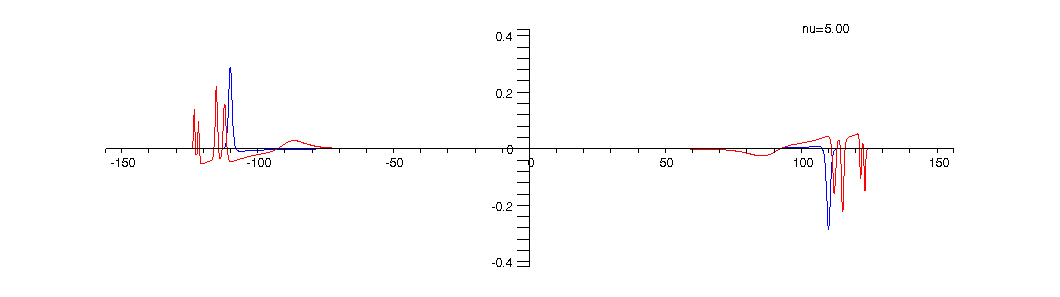
As can be seen from the above animations alternating compressible and incompressible strips are formed at the inner and outer edges of the ring when the filling factor (respectively the magnetic field) is varied.  The positions of the compressible strips are where the electron charge density changes rapidly, while the incompressible ones correspond to the regions between the compressible strips where the charge density is approximately constant. The peaks in the current density correspond to the compressible strips while in the incompressible channels the current is much smaller in amplitude and opposite in direction as compared to the peaks and the number of peaks corresponds to the number of (completely or partially) occupied Landau levels.